― ゆらぎ、止まれない量子 ―
水に垂らしたインクは自然に水に混ざっていく。アインシュタインによれば、これは分子の熱運動によるゆらぎによって生じている。では、もし熱が一切なかったら?熱がない世界ではゆらぎは起きないのだろうか。
水に垂らしたインクは自然に水に混ざっていく。アインシュタインによれば、これは分子の熱運動によるゆらぎによって生じている。では、もし熱が一切なかったら?熱がない世界ではゆらぎは起きないのだろうか。
1827年、R. Brownによって静止した水の中を花粉がランダムに移動する現象が発見されました。ブラウン運動と呼ばれるこの現象とそのランダムな振る舞いは、1905年、A. Einsteinによって、熱運動する分子との衝突で説明されました。熱によって生じるこうしたランダムな運動(「ゆらぎ」)は、水に垂らしたインクが混ざる現象、電気回路の中の雑音、さらには太陽が放つ光の色まで、非常に広い範囲の物理現象と関係しています。こうしたゆらぎは、熱運動によって生じていますから、冷やすことで小さくなることが知られています。それでは、周囲に分子のない完全な真空や、すべての粒子が静止した絶対零度の世界では、ゆらぎはないのでしょうか。
量子力学では、量子の位置と速度(運動量)との間に不確定性関係と呼ばれる、位置と速度が同時には決定されないという性質があります。
この性質を理解するため、粒子の波動関数について考えてみます。
他のコンテンツで説明されているように、量子力学では、量子の振る舞いを波動関数によって表します。
量子はそもそも重ね合わせ状態という異なる位置に同時に存在することができますから、その性質を表したものが波動関数になります。
波動関数とは、粒子が存在する確率が高い位置では大きな振幅をもち、全体に広がった波のようなものです。
一方で、量子力学によると、この波の「傾き」は速度を表します。
さて、それでは、位置のゆらぎが小さい粒子の波動関数について考えてみましょう。
図1の右の図がそんな波動関数を表したものになります。
粒子ゆらぎは小さいですから、波動関数は空間的に狭い場所で大きな振幅をもっていて、そこに集中していることになります。
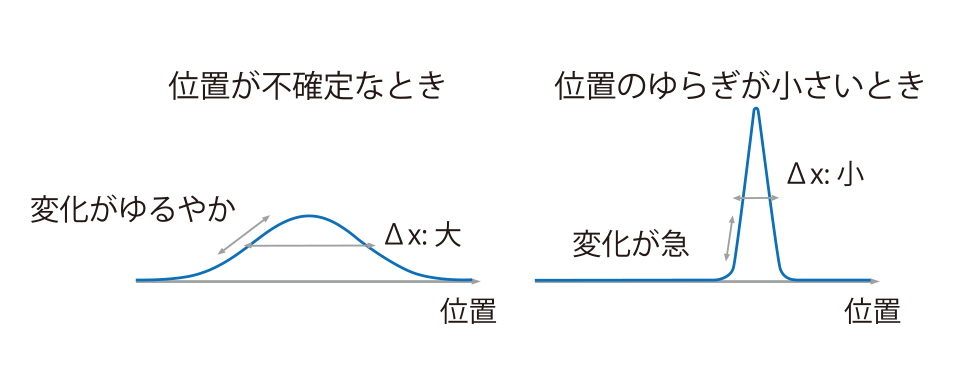
その場合、波動関数は空間的に急激に変化していることになりますから、波動関数の傾きは大きくなり、より大きな速度のゆらぎを持っていることになります。一方で、図1の左の図のように、位置のゆらぎが大きく、波動関数がなだらかなときは、その粒子の速度ゆらぎは比較的小さいことがわかります。このように、量子力学では、粒子の位置と速度との間にそのどちらかのゆらぎが小さくなると、もう片方が大きくなる性質があります。
それでは、粒子のゆらぎについて考えてみます。最初の節で触れたように、高温では熱によるランダムな分子の衝突によって、粒子はブラウン運動による大きなゆらぎを持ちます。そこで、冷却によって粒子の運動から熱に由来するものを取り除くことを考えます。周囲の温度が冷えることにより、粒子は熱によるランダムな動きが減っていき、どんどん止まっていきます。しかしながら、前の節で触れたように、量子力学においては、位置が確定した状態は大きな速度ゆらぎをもつことになります。速度をもった粒子は運動エネルギーを持つため、したがって位置が確定した状態は非常に高いエネルギーをもつことになります。その結果、温度を冷やしていっても、完全には止まらず、不確定性関係で決まる位置と速度のゆらぎの関係までしかゆらぎは小さくならないことが言えます。それ以上、位置のゆらぎを小さくしようとすると、反対に速度のゆらぎが増え、反対に粒子のエネルギーが増えてしまい、それらのトレードオフの関係によって最小のゆらぎが決まります。これを最小不確定状態と呼び、そのゆらぎを量子ゆらぎと呼びます。
